|
|
|
|
|
Galleria Tassonomica
di
Natura Mediterraneo
|
|
|
| Autore |
 Discussione  |
|
|
DanieleU
Utente Junior
Città: Compiano
Prov.: Parma
Regione: Emilia Romagna
55 Messaggi
Tutti i Forum |
 Inserito il - 18 novembre 2012 : 11:25:54
|
Nel topic "Creature alate e statistica" sono stati affrontati problemi di misura, a cui si può corrispondere ricorrendo alla statistica univariata (media, deviazione standard, intervallo di confidenza).
Sebbene le cose da dire, a proposito di questi metodi statistici elementari, siano ancora molte, a "volo d'uccello" propongo un altro approccio.
Quando si ha a che fare con piu' popolazioni ( piu' specie) che condividono il medesimo habitat, la ricerca si fa piu' complessa e necessita di un approccio multidisciplinare.
Nel medesimo habitat non ci sono mai situazioni di equilibrio: questo perchè convivono predatori e predati; perchè gli erbivori dipendono dall'evolvere delle stagioni, gli uccellimi dall'abbondanza di vermi, di larve, di bacche e i predatori dall'abbondanza del cibo di cui si nutrono.
Tutte le specie animali, poi, sono in relazione col suolo, con le trasformazioni biochimiche che esso subisce e che, spesso, è condizionato dall'impatto antropico.
Per indagare la vita di relazione in un habitat non basta la semplice osservazione di una specie. E' invece necessario un approccio multiplo, compiuto in piu' momenti, su diverse parcelle di territorio e magari anche in modo ricorsivo per piu' anni.
La mole di dati raccolta deve confluire in un dataset, funzionale al disegno sperimentale.
Questi dati devono poi essere convenientemente elaborati per comprendere l'abbondanza, i fattori di stress, le differenze quali-quantitative nei vari territori e, possibilmente potere trarre inferenze e compiere generalizzazioni sui dati ottenuti.
Da un punto di vista statistico è necessario ricorrere all'analisi fattoriale,a tecniche di kriging (su dati georeferenziati GIS) allo scopo di comprendere il "peso" e l'importanza dei vari fattori e delle variabili condizionate.
Mi riferisco alla cluster analysis ( PCA, CA,CCA, MCA ecc.) sia a tecniche di multiscaling o di Bootstrap ( Monte Carlo, randomForest, reti neurali....); il tutto che abbia come output dei dendrogrammi gerarchici che siano in grado di creare gruppi di similarità.
So molto poco di uccelli, ma immagino sarebbe utile costruire un sub-dataset ( parte di un dataset piu' complesso e che riguarda una pluralità di specie) in cui entrino variabili booleane, quantitative, e ordinali.
Per esempio una variabile booleana ( o dicotomica) potrebbe riguardare la presenza di uccelli classificati in stanziali e migratori ( 0=stanziali 1= migratori), poi altra variabile booleana che definisca se si tratti di uccelli diurni o notturmi ( 0= diurni 1= notturni), una variabile tassonomica che riguardi l'ordine(?) dei passeriformi o non passeriformi ( in questo caso sarebbe una variabile dicotomica asimmetrica, perchè: 0= passeriformi 1= tutte le specie non passeriformi).
A queste variabili si possono aggiungere variabili quantitative ( per esempio misure di aperture alari, peso corporeo, ecc.)oppure di conteggio relativo al numero dei soggetti contati su una data particella di territorio.
L'elaborazione può essere compiuta ricorrendo al software statistico ( open source, scaricabile in rete) "R". Questo software, è di fatto una "piattaforma" sulla quale si possono caricare numerose librerie, alcune delle quali dedicate alla ricerca ambientale, come "Vegan", "BiodiversityR", "eco", "ade4TkGUI" eccetera.
Come output è possibile ottenere sia report numerari ( distanza euclidea, di Manhattan, di Ward, coefficienti di stress, coefficienti di similarità e dissimilarità, di abbondanza ecc.)
Oltre ai classici output dell'analisi fattoriale ( Principal Corrispondence Analysis, Canonical Analysis.....)
oppure dendrogrammi e una serie di grafici molto esplicativi.
Lascio questo discorso in sospeso perchè, per la sua complessità, si presta a numerose considerazioni.
|
|
|
DanieleU
Utente Junior
Città: Compiano
Prov.: Parma
Regione: Emilia Romagna
55 Messaggi
Tutti i Forum |
Inserito il - 18 novembre 2012 : 15:01:00
|
Inserisco un esempio, scusandomi in anticipo perchè, essendo del tutto incompetente in ornitologia, magari ho individuato variabili non consone per una ricerca mirata sugli uccelli.
Ho previsto un dataset con le seguenti variabili: "specie, attitudine, migrazione, passeriforme, avvistati, inanellati, peso."
Le prime quattro variabili sono booleane ( a cui si risponde con "0" e "1")
Per "attitudine" ho inteso se sono diurni o notturn.
Con "migrazione" se si tratta di uccelli migratori oppure no.
"Passeriforme" è una variabile booleana asimmetrica, perchè "0" individua i passeriformi e "1" tutti gli ucceli diversi da passeriformi.
"avvistati" riguarda la presenza accertata in una definita unità di tempo ed in un dato luogo.
"inanellati" è intuitivo
"peso" in grammi il peso corporeo del volatile.
Ripeto: le variabili sono state definite da un incompetente, per cui possono benissimo essere sostituite con altrettante ( o piu') piu' indicative.
Definito il dataset l'ho caricato in "R" ed ho richiamato la libreria "cluster"
> library(cluster)
> data(uccelli)
> uc<-uccelli[1:7,]
> uc
specie attitudine migrazione passeriforme avvistati inanellati peso
1 passero 0 0 0 23 12 10
2 fringuello 0 0 0 5 3 8
3 pettirosso 0 0 0 13 6 14
4 picchio rosso 0 0 1 2 1 30
5 picchio verde 0 0 1 1 0 28
6 allocco 1 0 1 4 0 120
7 ballerina 0 0 1 8 0 20
Queste sono le prime sette righe del dataset con relative variabili.
Ora impartisco il comando "daisy" che serve a descrivere la dissimilarità, ed ottengo:
> daisy(uc, type=list(asymm=c(3)))
Dissimilarities :
1 2 3 4 5 6 7
2 0.4221893
3 0.3226395 0.2665679
4 0.6391636 0.3838167 0.4831908
5 0.6602110 0.4048641 0.5042382 0.1878898
6 0.8091800 0.5538331 0.6532072 0.3656686 0.3591139
7 0.6091349 0.3972663 0.4531621 0.2244731 0.2177427 0.3667117
NB. l'indicazione "asymm=c(3)" serve a istruire il sistema dicendo che la terza è una variabile asimmetrica (passeriforme)
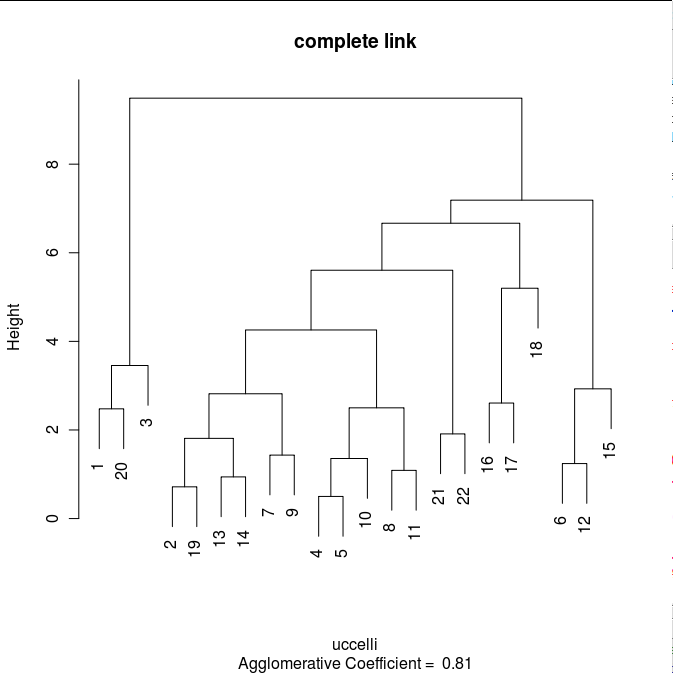
A questo istruisco il programma perchè restituisca il grafico del dendrogramma:
> ag<-agnes(uccelli, method="complete", stand=TRUE)
> plot(ag, main="complete link", which=2)
ed ottengo il dendrogramma
Immagine:
21,31 KB |
|
 |
|
|
DanieleU
Utente Junior
Città: Compiano
Prov.: Parma
Regione: Emilia Romagna
55 Messaggi
Tutti i Forum |
Inserito il - 18 novembre 2012 : 15:07:35
|
Ora è possibile vedere anche quali siano le componenti principali nei cluster e come si aggregano tra di loro.
Nei "rami" piu' bassi si trovano gli elementi piu' vicini; salendo, fino all'origine del dendrogramma, gli elementi piu' lontani o dissimili.
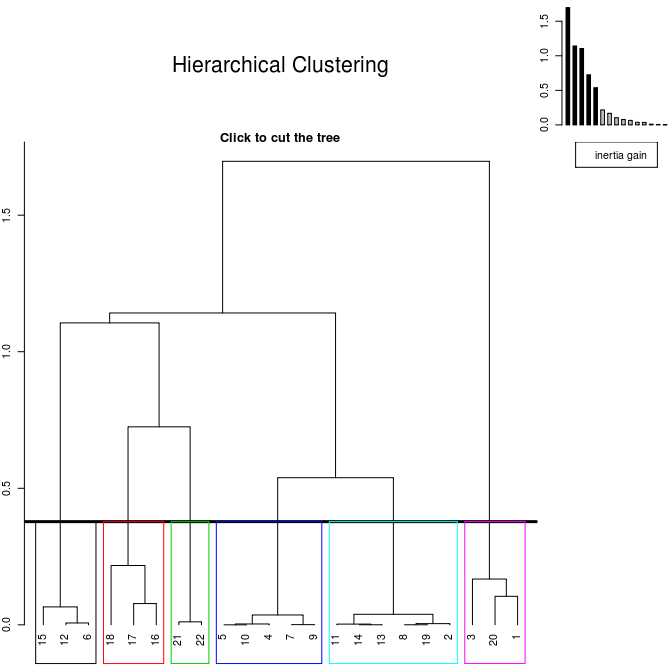
E' possibile anche ottenere dal sistema l'aggregazione dei cluster.
Dopo di che il dendrogramma si presenta in questo modo:
Immagine:
17,82 KB |
|
|
|
|
DanieleU
Utente Junior
Città: Compiano
Prov.: Parma
Regione: Emilia Romagna
55 Messaggi
Tutti i Forum |
Inserito il - 18 novembre 2012 : 15:24:51
|
Ora è possibile individuare le componenti principali.
Nelle ricerche ambientali si ha quasi sempre a che fare con variabili non normali.
Il ricercatore, nel monitorare le variabili da indagare si possono inserire variabili importanti ed attendibili e variabili di scarso peso.
A priori non si può sapere cosa sia importante e cosa no. Dunque l'analisi va fatta a posteriori, valutando il "peso" di ciascuna variabile.
Si valutano le componenti sugli assi principali.
Di solito il primo e secondo asse spiegano gran parte della varianza: elemento che si può vedere tramite gli eugivalues.
Questo è l'output garfico e numerario:
> res$eig
eigenvalue percentage of variance cumulative percentage of variance
comp 1 2.31847724 38.6412874 38.64129
comp 2 1.31457302 21.9095504 60.55084
comp 3 1.08159803 18.0266339 78.57747
comp 4 0.78314779 13.0524632 91.62993
comp 5 0.44757492 7.4595819 99.08952
comp 6 0.05462899 0.9104832 100.00000
$contrib
Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
attitudine 8.976227 3.514524 48.871359 13.19244354 25.417915271
migrazione 2.732948 33.391627 22.761879 20.52210922 20.237014055
passeriforme 13.239442 24.773684 10.960992 6.20947139 44.716692805
avvistati 34.145538 7.407447 7.486915 0.29272212 0.004411298
inanellati 32.183761 11.429064 6.558730 0.06570125 1.258421256
peso 8.722085 19.483654 3.360125 59.71755248 8.365545316
Le due tabelle precedenti mostrano il "peso" delle variabili sugli assi principali.
Si nota, per esempio che Dim1 ( il primo asse) spiega il 38,64% della varianza.
I primi due assi spiegano oltre il 60% della varianza totale.
La tabellina successiva mostra il contributo di ciascuna variabile al modello.
Per cui leggiamo che "avvistati", "inanellati" pesano per il 34% e il 32 % sulla varianza totale, relativamente al primo asse.
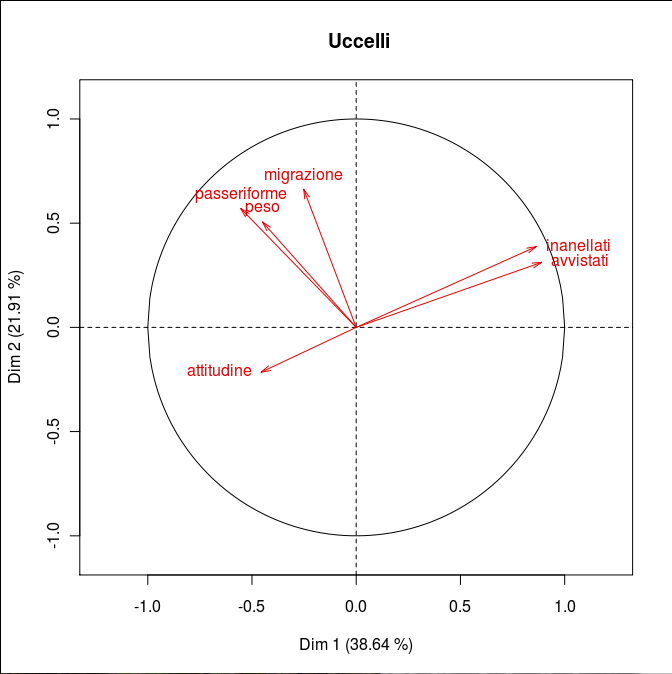
Il grafico successivo (pie) mostra come si collocano le variabili attorno agli assi principali.
Piu' le variabili sono vicine e piu' esprimono similarità e viceversa.
Immagine:
46,43 KB |
|
|
|
| |
Discussione |
|
|
|
 Natura Mediterraneo |
© 2003-2024 Natura Mediterraneo |
|
|
Leps.it | Herp.it | Lynkos.net
|
Forum
|
Registrati
|
Msg attivi
|
Msg Recenti
|
Msg Pvt
|
Utenti
|
Galleria |
Map |
Gadgets
|
Cerca
|
|
FAQ | Regole |
| 
| 
Suggerimento: Hai provato la nostra ricerca tassonomica da Browser? Clicca qui per info!
Statistica e ricerca ambientale
